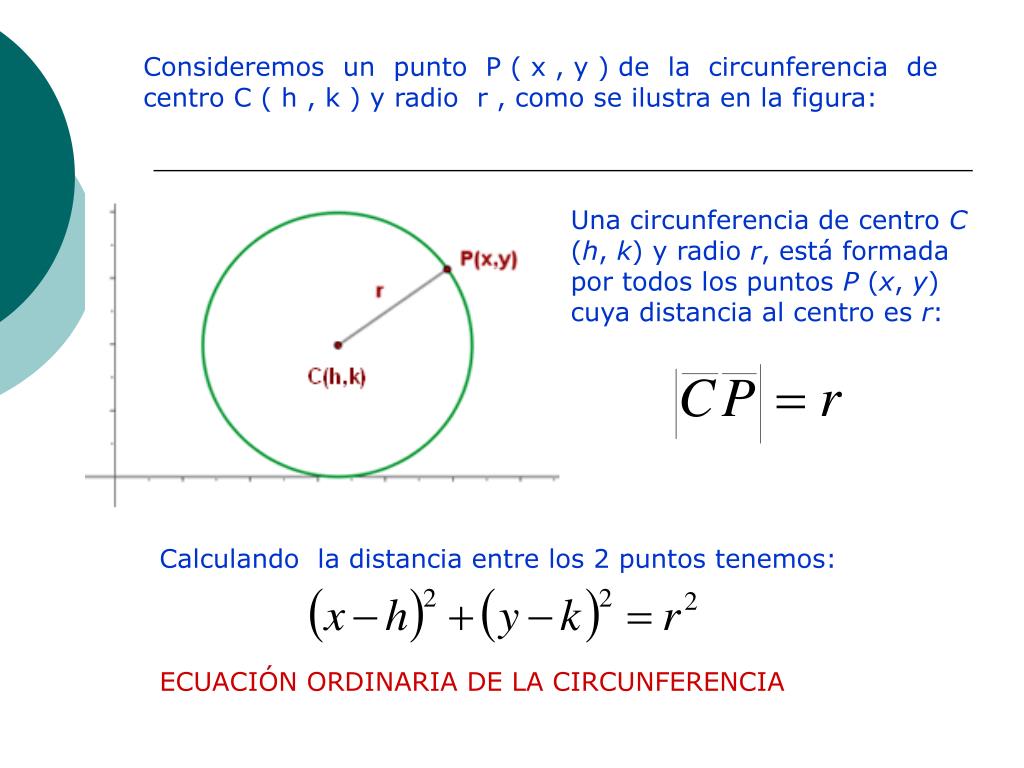
Formulas de la circunferencia
La circunferencia es una figura geométrica muy importante en matemáticas.
Es el conjunto de todos los puntos que equidistan de un punto llamado centro. En esta artículo, exploraremos algunas fórmulas útiles relacionadas con las circunferencias.
Longitud de circunferenncia circunferencia
La longitud de una circunferencia se puede calcular utilizando la fórmula:
L = 2πr
donde L representa la longitud de la circunferencia y r es el radio.
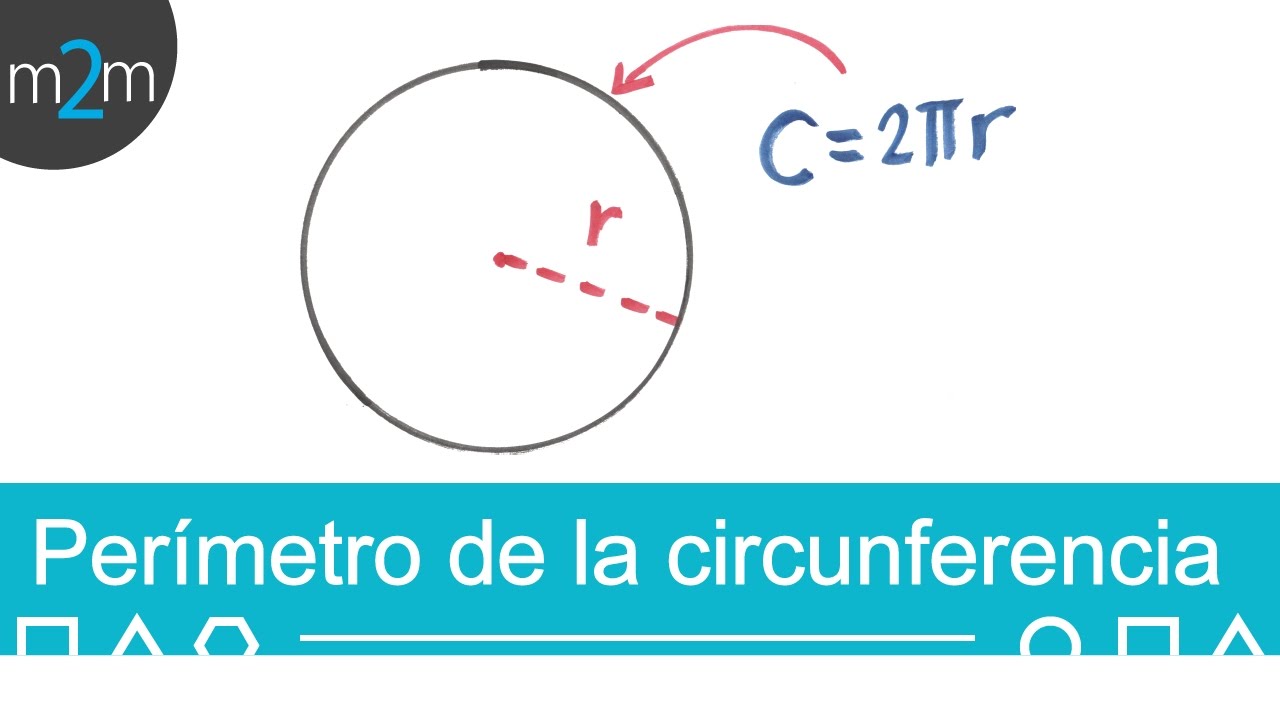
El valor de π es aproximadamente 3.14159, ce constante irracional que relaciona la longitud de una circunferencia con su diámetro.
Área de la circunferencia
El área de una circunferencia se puede encontrar utilizando la fórmula:
A = πr²
donde A representa el área de la circunferencia y r es el radio. Sabiendo que el radio es la Formulxs entre el centro de la circunferencia y cualquier punto de su perímetro, podemos calcular el área de forma sencilla.
Cálculo del radio y del diámetro
Si conocemos la longitud de una circunferencia, podemos encontrar el radio y el diámetro utilizando las siguientes fórmulas:
r = L / (2π)
d = 2r
donde r es el radio, L es la longitud de la circunferencia y d es el diámetro.
Relación entre circunferencia y recta
La recta que une dos puntos en el perímetro de una circunferencia se denomina cuerda.
Si trazamos una cuerda y la dividimos en ds partes iguales, obtenemos lo que se conoce como un diámetro.

La relación entre el diámetro y la cuerda se puede expresar mediante la siguiente fórmula:
d = √(4r² - c²)
donde d es el diámetro, r es el radio y c es la longitud de la cuerda.
Conclusión
Las fórmulas de la circunferencia son herramientas fundamentales en matemáticas.
Nos permiten calcular la longitud, el área, el radio, el diámetro y establecer relaciones entre la circunferencia y las cuerdas. A través del uso de estas fórmulas, podemos resolver problemas geométricos y comprender mejor las propiedades y características de las circunferencias.
Es importante recordar que estas fórmulas son útiles en cicunferencia contextos matemáticos y aplicaciones prácticas, como la física, la geometría y la ingeniería.