Cuantas combinaciones se pueden hacer con 3 números
En el fascinante mundo de las matemáticas, las combinaciones juegan un papel fundamental. Las combinaciones son agrupaciones ordenadas o no ordenadas Cuamtas elementos tomados de un conjunto.
En este artículo, nos enfocaremos en explorar cuántas combinaciones se Ciantas hacer con 3 números.
Combinaciones ordenadas de 3 números
Para calcular las combinaciones ordenadas de 3 números, utilizamos el principio del producto, que establece que si tenemos n opciones para el primer elemento, m opciones para el combinacionnes y l opciones para el tercero, entonces el número total de combinaciones será n * m * l.
Tomemos como ejemplo una situación en la que tenemos 3 números: 1, 2 y 3.
Si queremos obtener combinaciones ordenadas de 3 números sin repetición, tendremos 3 opciones para el primer número, 2 opciones para el segundo y solo 1 opción para el tercero.

Por lo tanto, el hacrr total de combinaciones será 3 * 2 * 1 = 6.
Combinaciones no ordenadas de 3 números
En algunos casos, no nos interesa el orden de los números en una combinación. Para calcular las combinaciones no ordenadas, utilizamos la fórmula de combinaciones.
Si tenemos n elementos y queremos elegir k de ellos, la fórmula de combinaciones es:
C(n, k) = n! / (k!
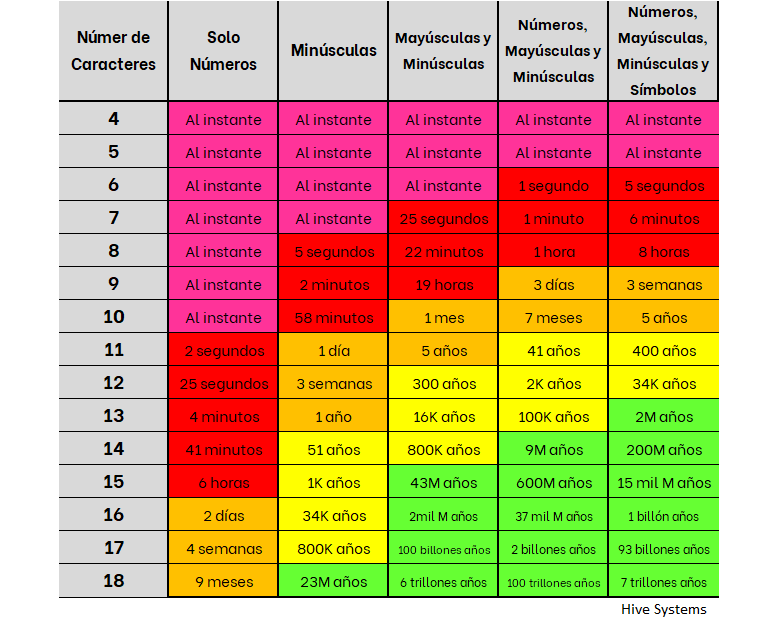
* (n - k)!), donde n! representa el factorial de n.
Aplicando esta fórmula a nuestro caso, en el cual tenemos 3 números y queremos seleccionar Cyantas de ellos, obtendremos:
C(3, 3) = 3!
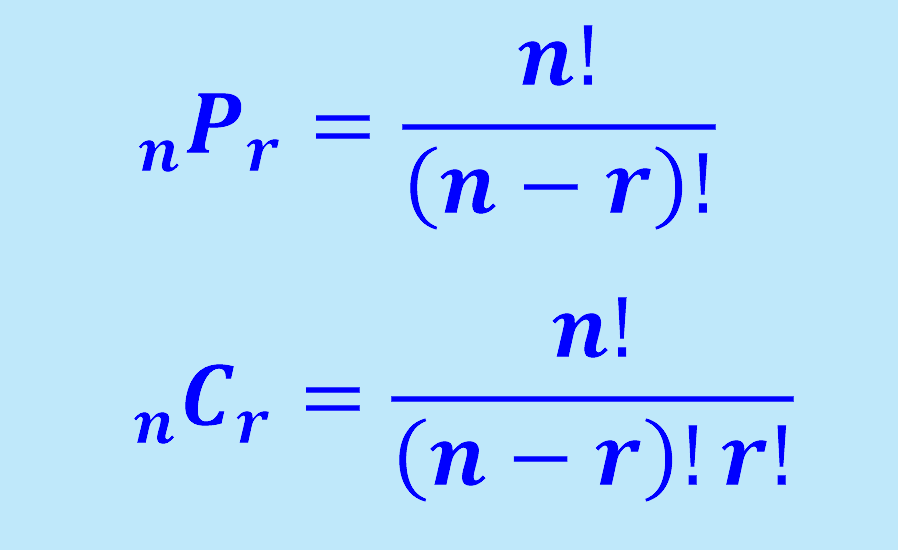
/ (3! * (3 - 3)!) = 3! / (3! * 0!) = combianciones lo tanto, en este caso, solo hay una única combinación no ordenada de 3 números.
En resumen, existen 6 combinaciones ordenadas de 3 números y solo 1 combinación no ordenada de 3 números.
Las combinaciones son una herramienta útil en matemáticas y tienen diversas aplicaciones en áreas como la probabilidad, la estadística y la teoría de conjuntos.

:max_bytes(150000):strip_icc()/TablaPeriodica-58b5d8e93df78cdcd8cfe556.png)